陽解法のプログラムであるimpactを用いて梁の計算を行ってみました。
(同じものをCalculiX(陰的)で実施 A160_0 片持ち梁の解析 動解析)
対象 片持ち梁 シェル要素
モデル化 : FreeCADにてモデル化
計算ソルバー : impact(Version: 706042)
条件 : 計算シートの内容に準拠(K052 片持ち梁 曲げについて 計算)
梁断面 10㎜×10㎜ ヤング率 210000MPaとしている。
密度 7.9e-9 ton/mm^3
拘束 左端を完全固定
荷重 右端に下向きZ1000Nを等分布に設定
解析時間:全時間 0.01秒
結果出力間隔 0.0001秒
計算ステップタイム 1.25E-6秒
結果
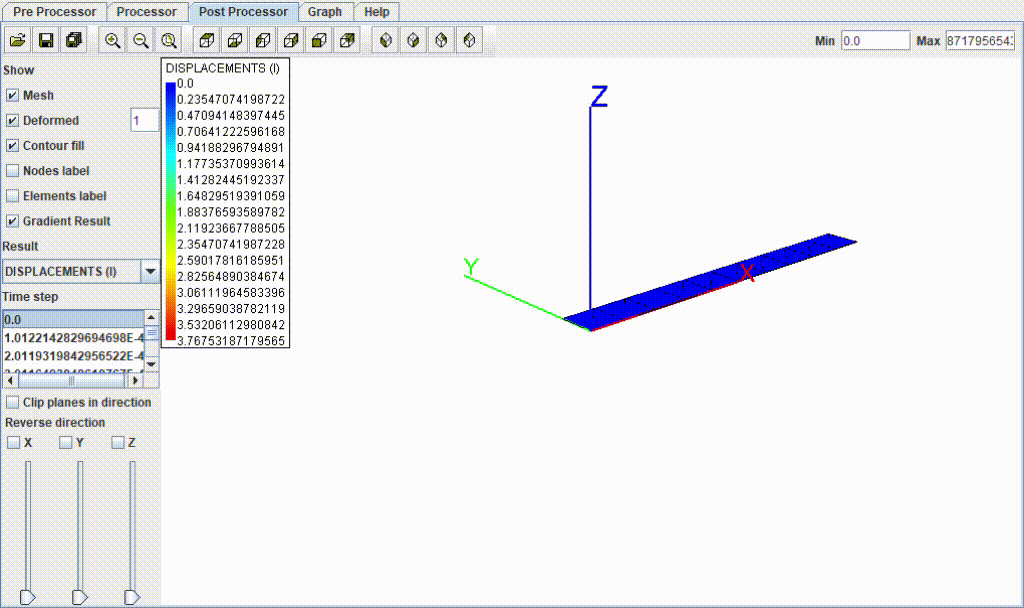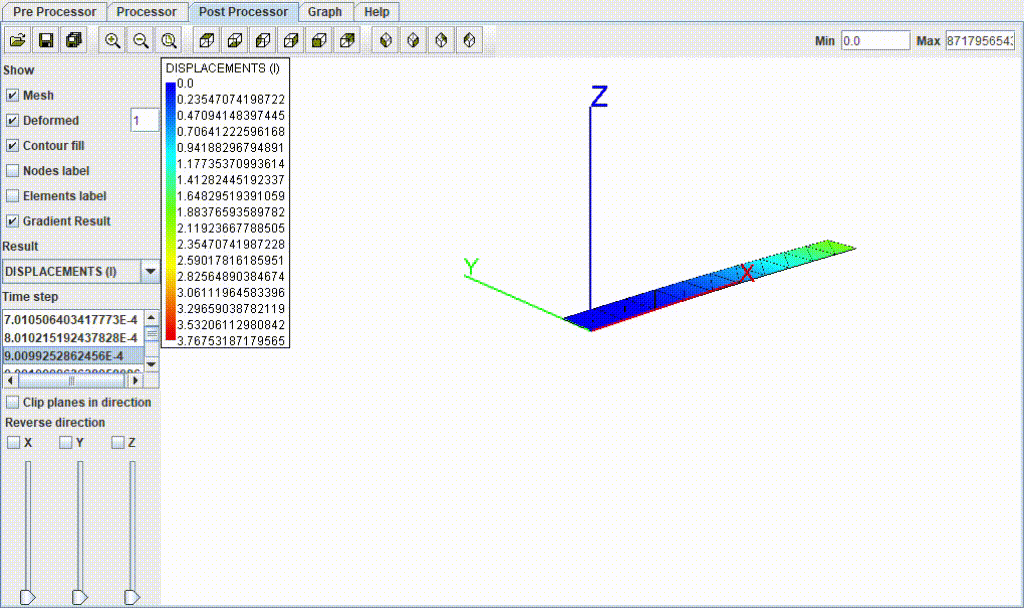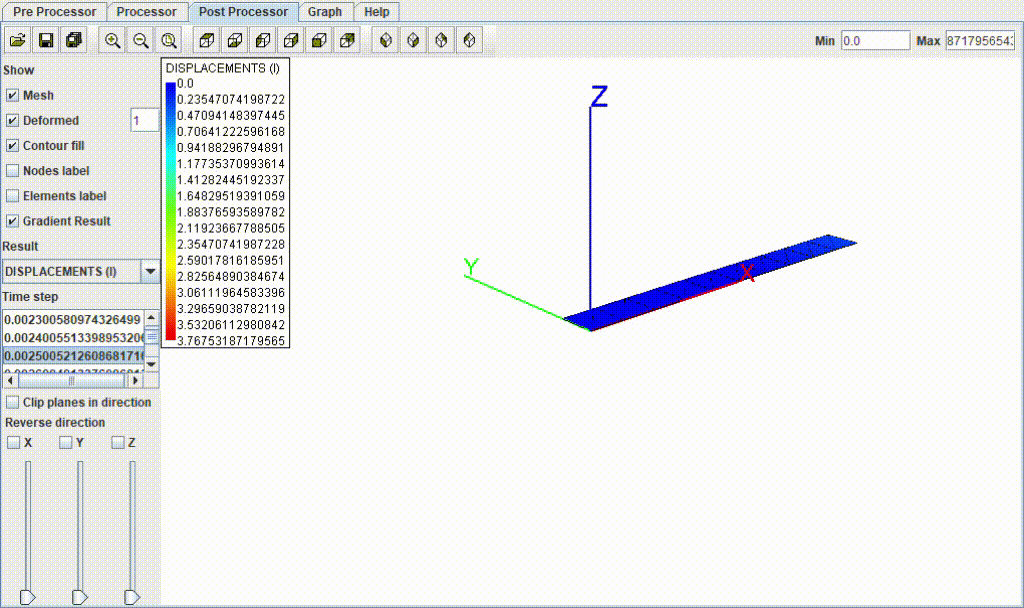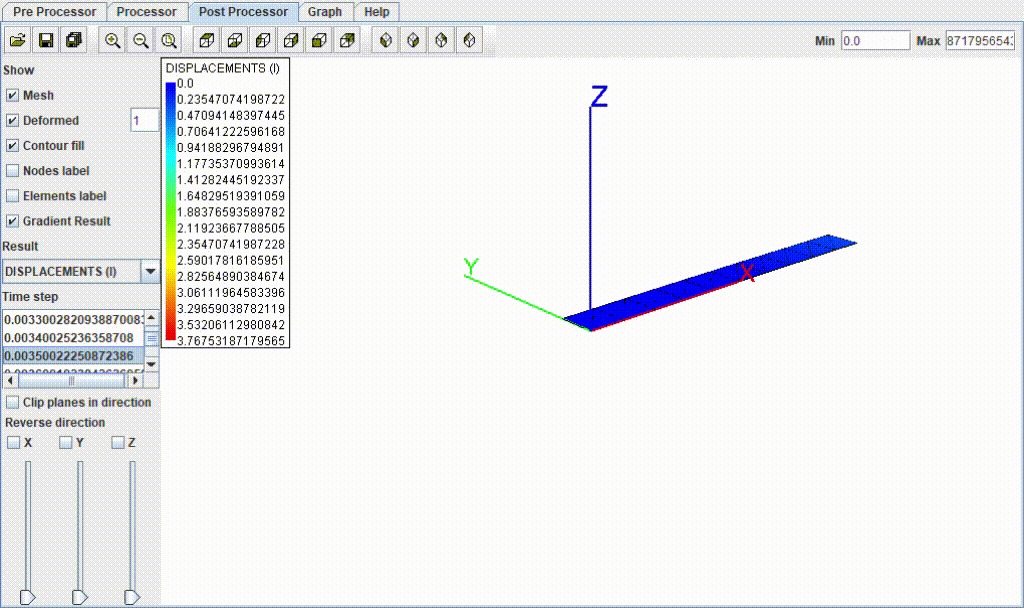
| 項目 | 値 |
| たわみ量 | 3.74 mm |
| 応力 | 68.59 MPa |
・シェル要素の確認
板要素は出力が縁ではなく実要素上の値を返していると思われます。
中立軸から外縁5mmを考慮すると以下となります。
68.59 × 5㎜ = 342.95 MPa(縁応力)
衝撃荷重として扱われているので、変位の結果についてはおよそ一致しています。(1.9×2 = 3.8mm)応力については、かなり乖離しています。(1200MPa)
応力については、要素形状(粗さ)、拘束条件の検討が必要そうです。
補足
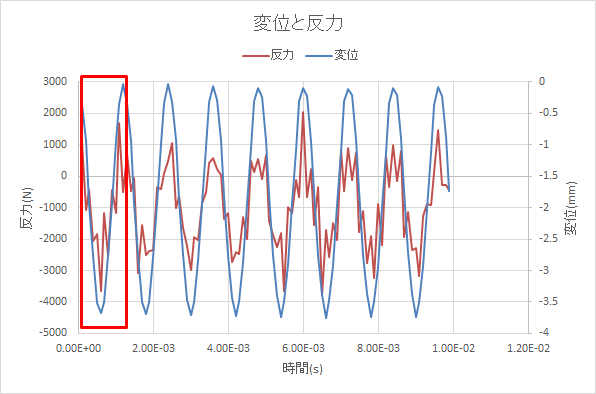
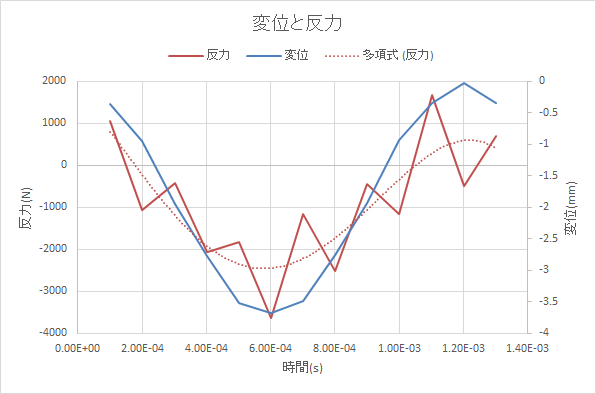
左端の固定端での反力と右端の節点変位のグラフになります。
1周期はおおよそ1次固有値と一致します。(1/1.2e-3 = 833Hz)
反力の値がデータのままだとかなり大きくでています(最大2000N)。波形処理(近似線)だとそこそこの値になります。減衰等の検討がいるかもしれません。設計上は応力よりも荷重結果を処理して用いた方が無難かもしれません。
参考:K061 衝撃荷重の計算
サンプルファイル(シェル要素) beam_shell_impact.in
作業
サンプルファイル:T160_tria.unv
そっと負荷する場合
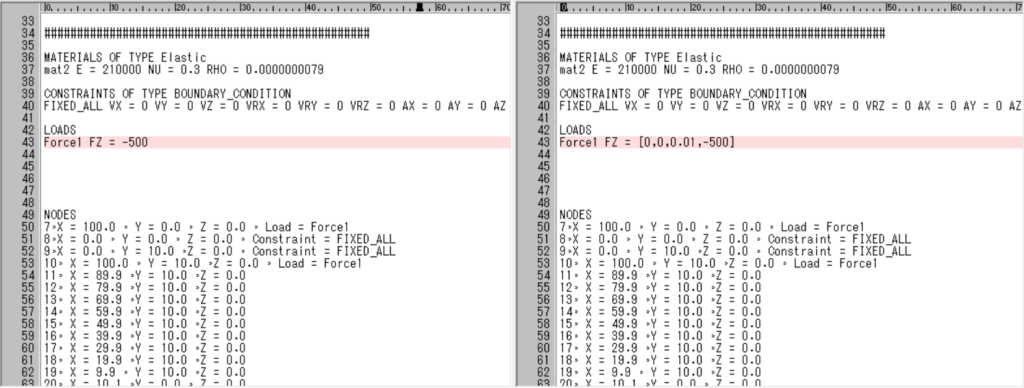
荷重の定義を Force1 FZ = -500 から Force1 FZ = [0,0,0.01,-500] に変更します。
時間0の時は0で、0.01秒に-500N(2か所)になるようにしています。荷重は直線的に増加します。
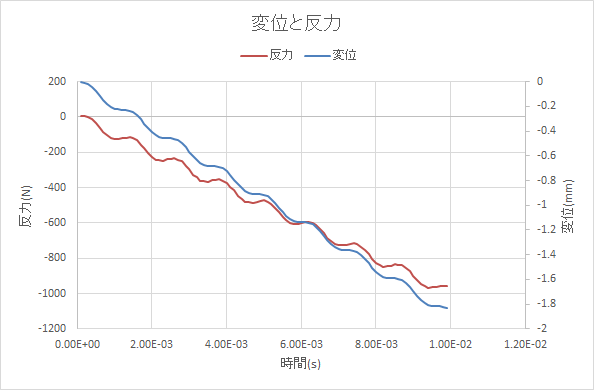
振動はしますが、1000Nで1.8mm程度のたわみ量でした。
おおよそ合っています。K052 片持ち梁 曲げについて 計算
tracker
データの取り出しはtrackerを設定して取り出します。(Cドライブに直下(C:\)にtrkファイルを作成する場合)[***]内の番号は節点番号です。参考:T303 impact tips Tracker
################################################## trackers of type nodeforce 1 nodes = [8,9] direction = z- filename = C:\nodebase_neg_tria.trk 2 nodes = [8,9] direction = z+ filename = C:\nodebase_pos_tria.trk 3 nodes = [8,9] direction = z- filename = C:\nodetop_neg_tria.trk 4 nodes = [8,9] direction = z+ filename = C:\nodetop_pos_tria.trk 12 nodes = [8] direction = z- filename = C:\nodebase_neg_tria1.trk 13 nodes = [9] direction = z- filename = C:\nodebase_neg_tria2.trk 14 nodes = [8,9] direction = z filename = C:\nodebase_tria.trk trackers of type energy 5 type = external filename = C:\energy_external_tria.trk 6 type = internal filename = C:\energy_internal_tria.trk 7 type = contact filename = C:\energy_contact_tria.trk 8 type = hourglass filename = C:\energy_hourglass_tria.trk trackers of type nodedisplacement 9 node = [7] direction = z filename =C:\disp_tria.trk target = [0.0058,0.00001,0.0,0.0001] trackers of type NodeVelocity 10 node = [7] direction = z filename = C:\nodebase_vel_tria.trk trackers of type nodeacceleration 11 node = [7] direction = z filename = C:\nodeacc_tria.trk ##################################################
コメント