応力について整理しておくページです。
解析(FEM)から
解析のデータだと分かりやすいのでサンプルとして使用します。
両持ち梁の曲げデータを使用します。
参照:A112 両持ち梁 曲げ
サンプルファイル:009_beam_double_stress-CCX_Results.vtk
(A112 両持ち梁 曲げ データから拘束をすこし変更しています)
(以下ParaViewで表示)
ミーゼス応力 von_Mises_Stress
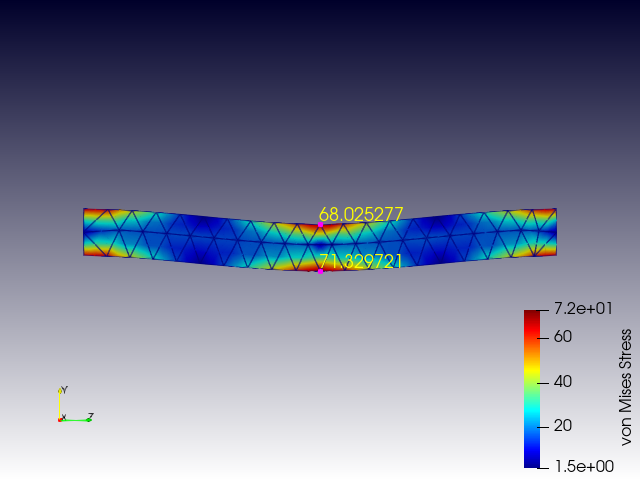
最大ひずみエネルギー説とも言います。せん断ひずみエネルギーが限界値になったら破損すると考えます。
延性材料によく用いられます。一番用いられるのではないでしょうか。
最大主応力 Major_Principal_Stress
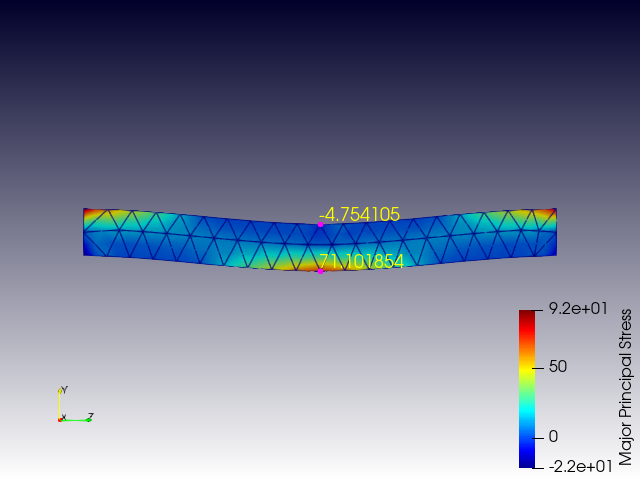
引張を確認したりするために使用します。
評価用では、鋳鉄、コンクリート、ガラスなどの脆い材料(脆性材料)に適用したりします。(最大主応力説)
最小主応力 Minor_Principal_Stress
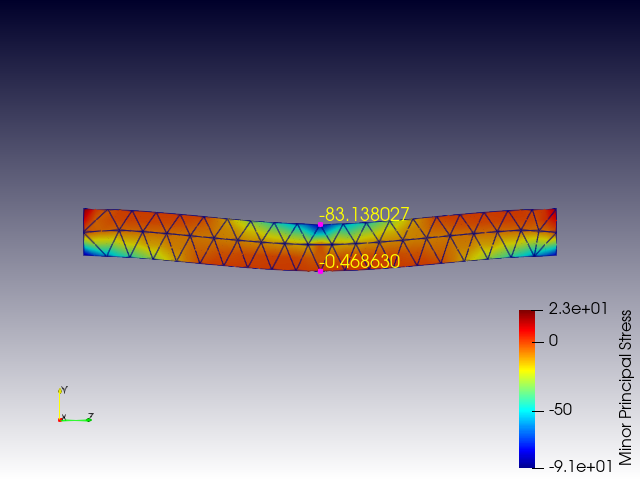
圧縮を確認したりするために使用します。
上図では、荷重負荷点が圧縮されているため、圧縮側に大きな値が確認できます。
トレスカ応力 Tresca Stress
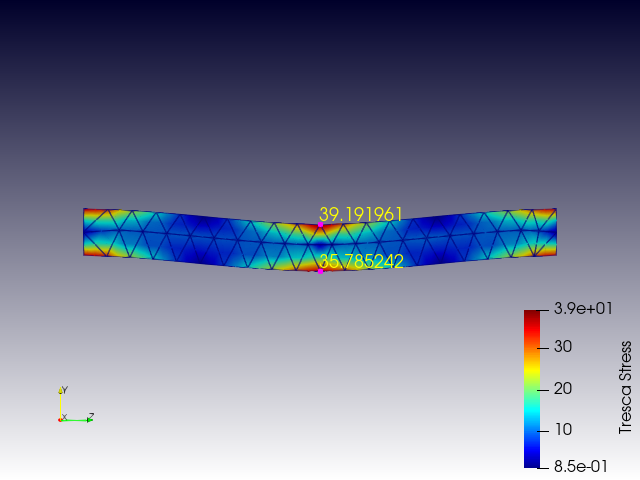
最大せん断応力説
金属材料の降伏は平均応力に依存しないので,材料に作用
している最大せん断応力、すなわち三つの主応力の差の絶対値のいずれかが材料
のせん断降伏応力に達したとき降伏するという考えです。
τ=(σmax-σmin)/2
・比較的伸びの大きい材料に適用されます。
・他の評価より限界応力がやや低めに得られ、設計上安全側になります。
更新中。。。
コメント