K091 ポアズイユ流れの計算

このツールは、二枚の平行な平板の間を流れる流体（ポアズイユ流れ）を物理法則に基づいてシミュレーションし、視覚的に理解を深めるためのインタラクティブな学習ツールです。 ポアズイユ流れは、管内の血液の流れや潤滑油の挙動など、身の回りの様々な現象に応用される流体力学の基本的なモデルです。

使い方

🔧 物理パラメータでは、平板間の距離 h や圧力差 ΔP などを変更できます。例えば、圧力差を大きくしたり、流体の粘度 μ を小さくすると、流れが速くなる様子がリアルタイムで確認できます。

🎨 描画設定では、シミュレーションに使われる粒子の数や大きさを調整し、見た目を変更できます。これらの設定は物理計算には影響しません。

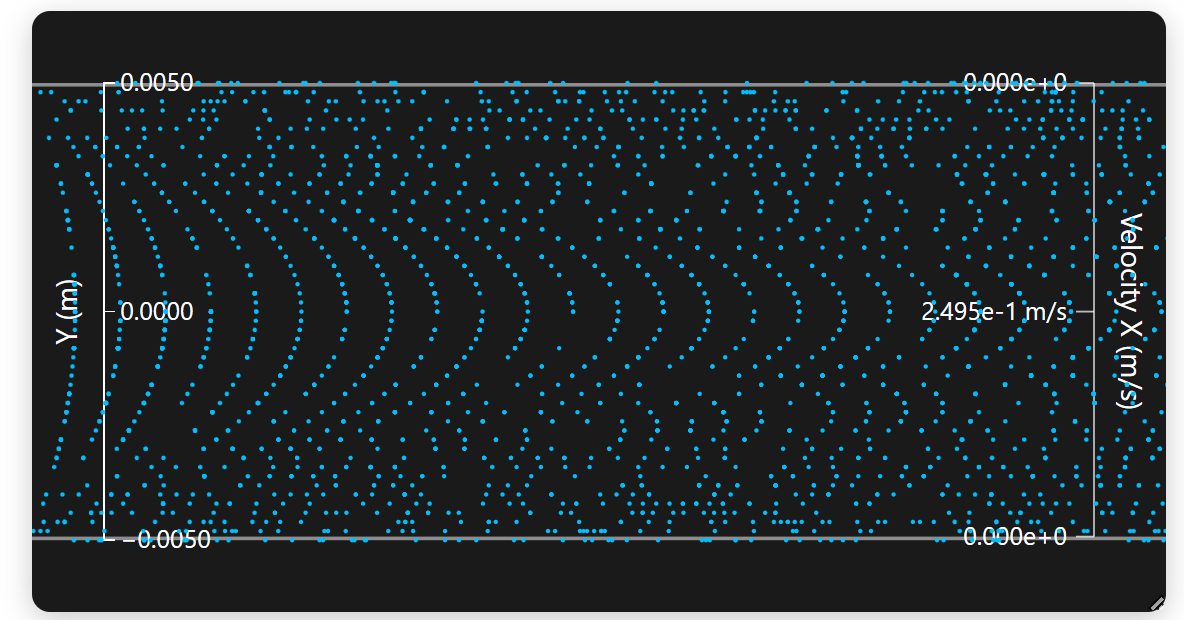
📊 下部に表示されるグラフは、流れの断面における「流速プロファイル」を示しています。理論通り、壁面（上下）で流速がゼロになり、中央で最も速くなる放物線状の分布になっていることが分かります。グラフ下のテキストエリアには、プロットに使用された座標と流速のデータがCSV形式で表示され、コピーして利用できます。

↔️ シミュレーション画面の右下隅をドラッグすることで、表示サイズを自由に変更できます。

基礎方程式

このシミュレーションで再現されている放物線状の流速プロファイルは、以下のナビエ–ストークス方程式の単純な形で表されます。

• u(y): 平板の中心からの距離 y における流速
• ΔP: 流れの始点と終点の圧力差
• L: 流れの距離
• μ: 流体の粘度
• h: 平板間の距離
• y: 平板の中心を0としたときのy座標 ( 範囲: -h/2 から +h/2 )

この式から、流速は壁面（y = ±h/2）で0となり、中心（y = 0）で最大値をとることが分かります。