旧版から、LLMで作成したコードでリプレイスしています。旧版は次ページ。
角度が変更できるようになっています。角度0度は旧版と同じ解析解を求めています。
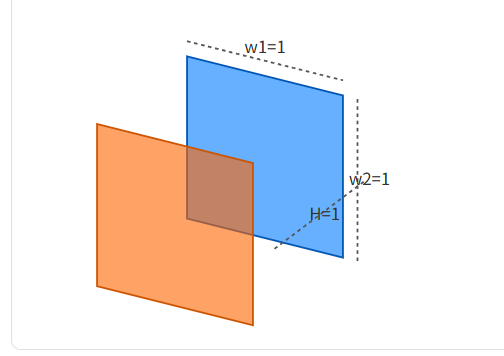
輻射の検討に必要な、平行な四辺形の形態係数(K090 形態係数)の確認計算を行います。
形態係数 (F12) =
- [-]
正面図
下面図
角度変更時の処理は統計的な推定によって計算しています。そのため再計算しても完全に再現はされません。(N=30000固定)誤差を小さくするには、グラフ計算用サンプル数を調整してください。
形態係数 $F_{12}$ は、面1から放出された全放射エネルギーのうち、面2に直接到達する割合を示す無次元量です。その値は、両面の幾何学的関係のみに依存します。一般的に、形態係数は以下の積分式で定義されます。
$$ F_{12} = \frac{1}{A_1} \iint_{A_1 A_2} \frac{\cos\beta_1 \cos\beta_2}{\pi r_{12}^2} dA_1 dA_2 $$ここで、$A_1$は面1の面積、$r_{12}$は面1の微小面積$dA_1$と面2の微小面積$dA_2$の間の距離、$\beta_1$と$\beta_2$は、それぞれの面の法線と2つの微小面積を結ぶ直線がなす角度です。
注記
角度は整数での入力になっています。
計算の仕組みがモンテカルロ法で乱数を用いたシミュレーションであり、計算結果は近似値です。
(3DCGのレイトレーシングのようなもの)
現状の設定だと、角度入力の精度にあまり意味がないので実数入力としていません。
覚書
可能なら数値積分を導入
Elmerと比較
拡張版

コメント