軸の曲げについて記載
(類似解析:A112 両持ち梁 曲げ)
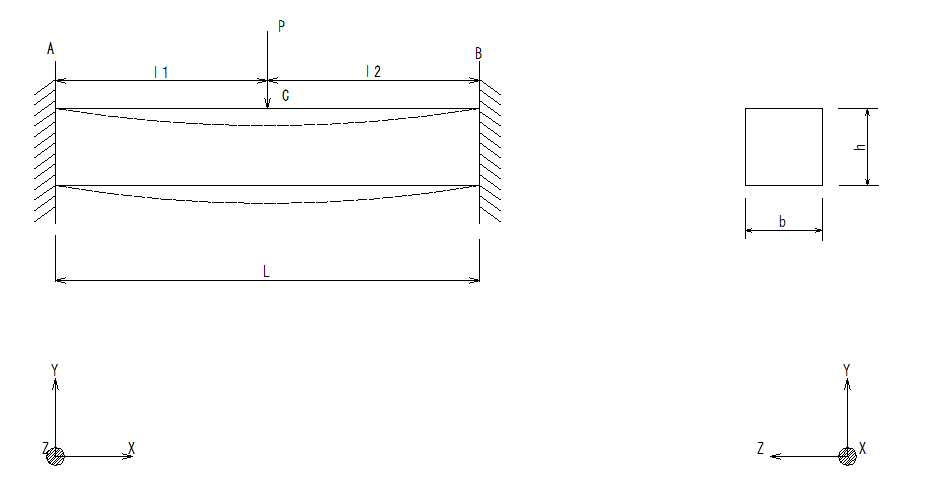
(1-1) はA地点の反力,(1-2) はB地点の反力です.
\begin{align}
\small Ra = \frac{P\cdot l2^2}{L^3}(3\cdot l1+l2) \tag{1-1} \\
\end{align}
\begin{align}
\small Rb = \frac{P\cdot l1^2}{L^3}(l1+3\cdot l2) \tag{1-2}
\end{align}
(2-1)はA地点のモーメント,(2-2)はB地点のモーメント、(2-3)はC地点のモーメントです.
\begin{align}
\small Ma = -\frac{P\cdot l1\cdot l2^2}{L^2} \tag{2-1} \\
\end{align}
\begin{align}
\small Mb = -\frac{P\cdot l1^2\cdot l2}{L^2} \tag{2-2}
\end{align}
\begin{align}
\small Mc = \frac{2P\cdot l1^2\cdot l2^2}{L^3} \tag{2-3}
\end{align}
(3-1)はL1>L2の変位,(3-2)はL1<L2 の変位です.
\begin{align}
\small ⊿max= \frac{2P\cdot l1^3\cdot l2^2}{3EI(3\cdot l1 + l2)^2} \tag{3-1} \\
\end{align}
\begin{align}
\small ⊿max= \frac{2P\cdot l1^2\cdot l2^3}{3EI(l1 + 3\cdot l2)^2} \tag{3-2} \\
\end{align}
| 部位 | 長さ(mm) |
|---|---|
| L1 | |
| L2 | |
| b | |
| h |
| 荷重 | 入力値(N) |
|---|---|
| P |
| 項目 | 入力値(N/mm2) |
|---|---|
| ヤング率 E |
| 項目 | 結果値 |
|---|---|
| 変位 | (mm) |
| 応力A | (N/mm2) |
| 応力B | (N/mm2) |
| 応力C |
(N/mm2) |
内訳HOLD
コメント