旧版から、LLMで作成したコードでリプレイスしています。旧版は次ページ。
（参考：A410 座屈の解析）
計算入力パラメータ
mm
N/mm2
例: 一端固定 m=0.25, 両端回転フリー m=1, 両端固定 m=4
断面二次モーメント I
以下のいずれかの方法で断面二次モーメント I を指定してください。
方法1: 矩形断面の寸法から自動計算 (こちらが優先されます)
mm
mm
方法2: I の値を直接入力 (幅bと高さhが空欄の場合に適用)
mm4
中間計算・断面形状情報
断面積 A
...
mm2
計算に使用される断面二次モーメント I
...
mm4
計算出力結果
最小座屈荷重 Pcr
...
N
以下は補足情報です。
断面二次半径 k
...
mm
細長比 λ
...
相当細長比 λr
...
計算レポート
概要
柱や梁のような縦に長い構造が軸方向（長手方向）の圧縮負荷を受けた際、ある限界の力を超えると、横方向に大きく曲がり急激に変形する「座屈」という現象が発生します。
このツールでは、この座屈現象が生じる最小の軸方向荷重である「最小座屈荷重 Pcr」を計算します。
座屈現象のイメージ
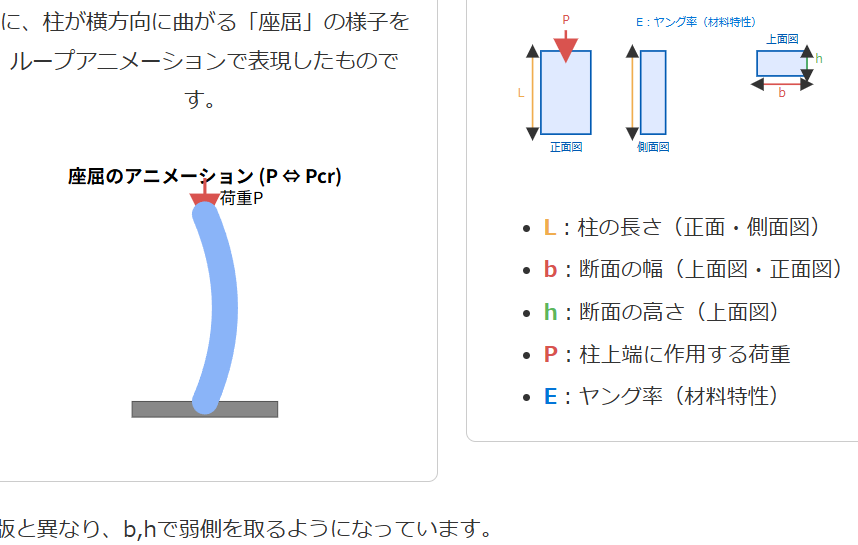
下の図は、荷重Pが臨界点Pcrに達した際に、柱が横方向に曲がる「座屈」の様子をループアニメーションで表現したものです。
入力パラメータの説明図（三面図）
- L：柱の長さ（正面・側面図）
- b：断面の幅（上面図・正面図）
- h：断面の高さ（上面図）
- P：柱上端に作用する荷重
- E：ヤング率（材料特性）
旧版と異なり、b,hで弱側を取るようになっています。
計算式
細長い柱（細長比が大きい場合）の最小座屈荷重 Pcr は、以下の「オイラーの座屈荷重式」によって計算されます。
\[ P_{cr} = \frac{m \pi^2 E I}{L^2} \]
固定定数 m と境界条件
計算式中の固定定数 m は、柱の両端がどのように支持されているか（境界条件）によって決まります。支持方法が違うと、柱の曲がりやすさが変わり、座屈のしやすさも変化します。以下に代表的な境界条件と、それに対応する m の値を示します。
依存関係図 (模式図)
下の図は、このページの計算要素（概念、入力、計算式、出力）がどのように関連しているかを示しています。ノードはドラッグして動かせます。
コメント