座屈の計算について記載します。(参考:A410 座屈の解析)
縦に長い構造は軸方向に負荷を受けた場合急激に変形することが起きます。そのような現象になる最小座屈荷重\( \small
Pcr\)がいくらであるかを確認します。
梁であれば、オイラーの座屈荷重(細長比:大)として以下の式があります。
\begin{align}
\small Pcr =\frac{m\cdot π^2\cdot E\cdot I}{l^2} \tag{1-1}
\end{align}
Iは最も弱くなるように、bとhを定めます。(断面二次半径の小さい方)Δ1
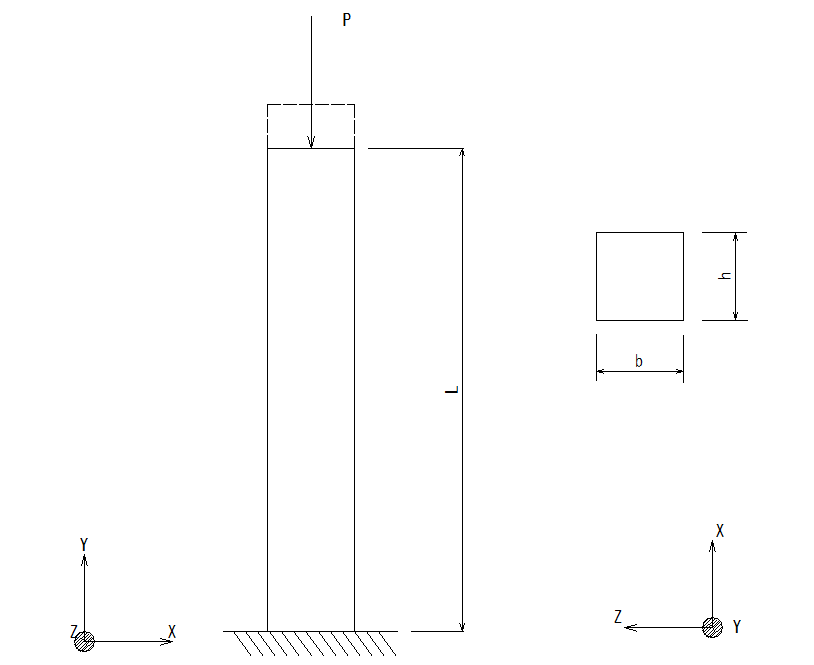
| 部位 | 長さ(mm) |
|---|---|
| L | |
| b | |
| h |
| 項目 | 入力値 |
|---|---|
| ヤング率 | N/mm2 |
| 項目 | 入力値 |
|---|---|
| m |
| 項目 | 結果値 |
|---|---|
| 面積 A | mm2 |
| 断面二次モーメント I | mm4 |
| 項目 | 結果値 |
|---|---|
| 最小座屈荷重 Pcr | N |
| 項目 | 結果値 |
|---|---|
| 断面二次半径 k | mm |
| 細長比 λ | |
| 相当細長比 λr |
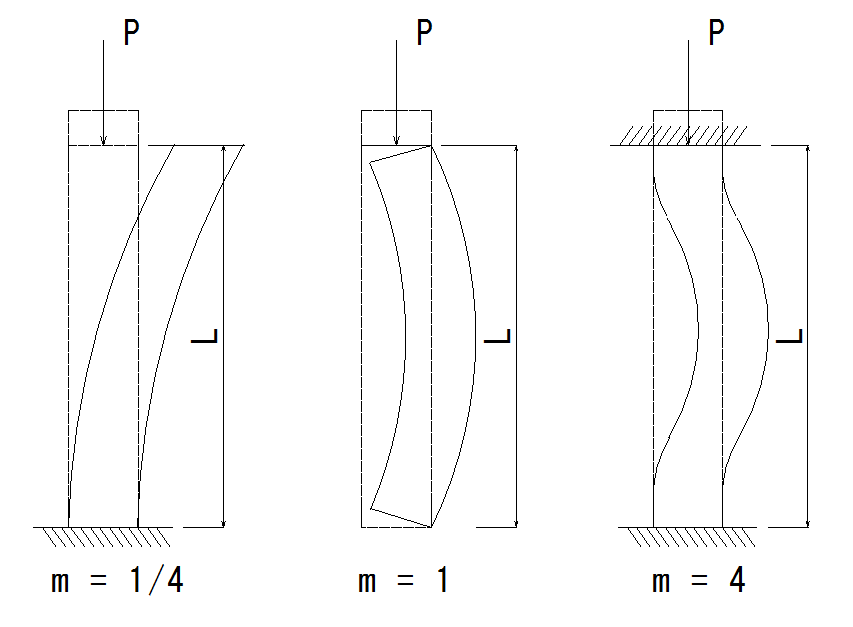
固定方法によるm違い
一端固定はm = 1/4(0.25)、両端回転フリーはm = 1、両端固定はm = 4。
Δ1:断面二次モーメントを任意入力にしました。(最弱方向のIを入力します)
コメント