旧版から、LLMで作成したコードでリプレイスしています。旧版は次ページ。
熱伝導のオーダーチェック用
(参考:ccxでの計算 A630 熱伝導解析)
(参考:Elmerでの計算 A631 熱伝導解析 Elmer(kg m系))
(参考:openFoamでの計算 A632 熱伝導解析 openFoam(kg m系))
計算ツール
計算結果
- 全長: mm
- 全計算時間: s
- 温度拡散係数 (α): mm²/s
- 安定性指標 (θ): [-]
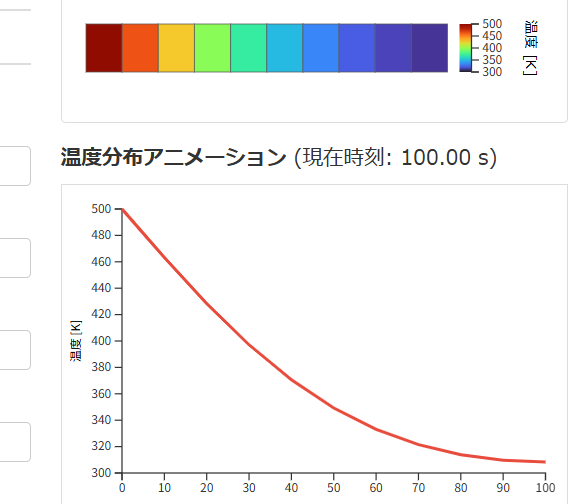
模式図アニメーション
温度分布アニメーション (現在時刻: 0.00 s)
計算データ
伝熱(熱伝導)とは?
伝熱とは、熱エネルギーがある場所から別の場所へ移動する現象全般を指します。この伝熱には、「熱伝導」「対流」「放射(輻射)」の3つの形態があります。
このツールで扱う熱伝導は、主に固体内部で熱が伝わる現象です。物質を構成する原子や分子がその場で振動し、その振動が隣の粒子へと次々に伝わることでエネルギーが移動します。
計算の原理 🧠
この計算は、フーリエの法則を基礎とする熱伝導方程式を、有限差分法という数値解析の手法を用いて解いています。時間と空間を微小な区間に分割し、各点での温度をステップバイステップで計算します。
1. 熱伝導方程式(一次元)
2. 温度拡散係数 (\(\alpha\))
3. 計算の安定性を示す無次元数 (\(\theta\))
一般的に、この \(\theta\) の値が 0.5以下でないと、計算結果が発散する可能性があります。
コメント