対象 梁 ソリッド要素
モデル化 FreeCADにてモデル化
条件 計算シートの内容に準拠(K041 断面性能 四角断面)
梁断面 10㎜×10㎜ ヤング率 210000MPaとします。
参照元 A110 例題A 片持ち梁の解析 のソリッドデータを引張として使用
境界条件 端面を強制変位で引っ張ります。
計算水準
a. 元の物性値のまま使用 ヤング率 ポアソン比
*ELASTIC
210000, 0.300
b. Ramberg-Osgood 則の使用
*DEFORMATION PLASTICITY
210000.,.3,800.,12.,0.4
c. SS線を定義 弾性部はaのまま、塑性部を追加
*ELASTIC
210000, 0.300
*PLASTIC
800.,0.
1100.,0.03
結果
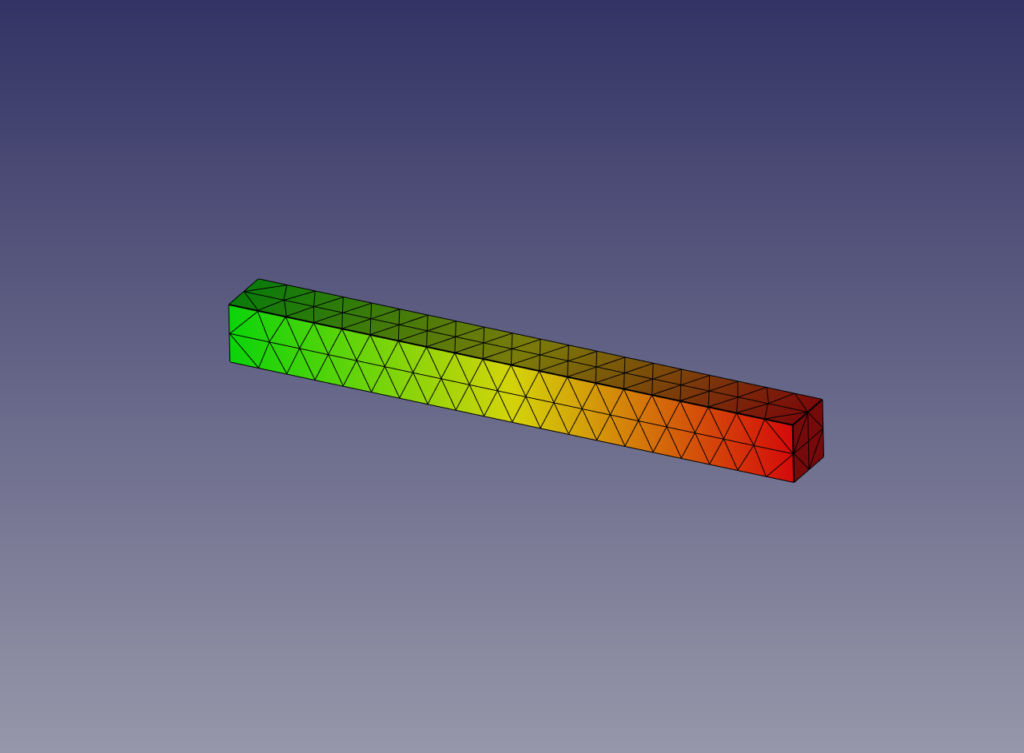
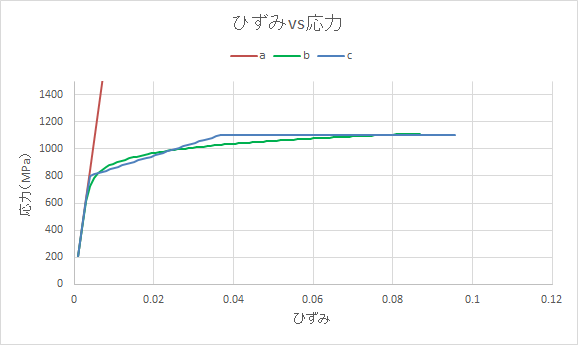
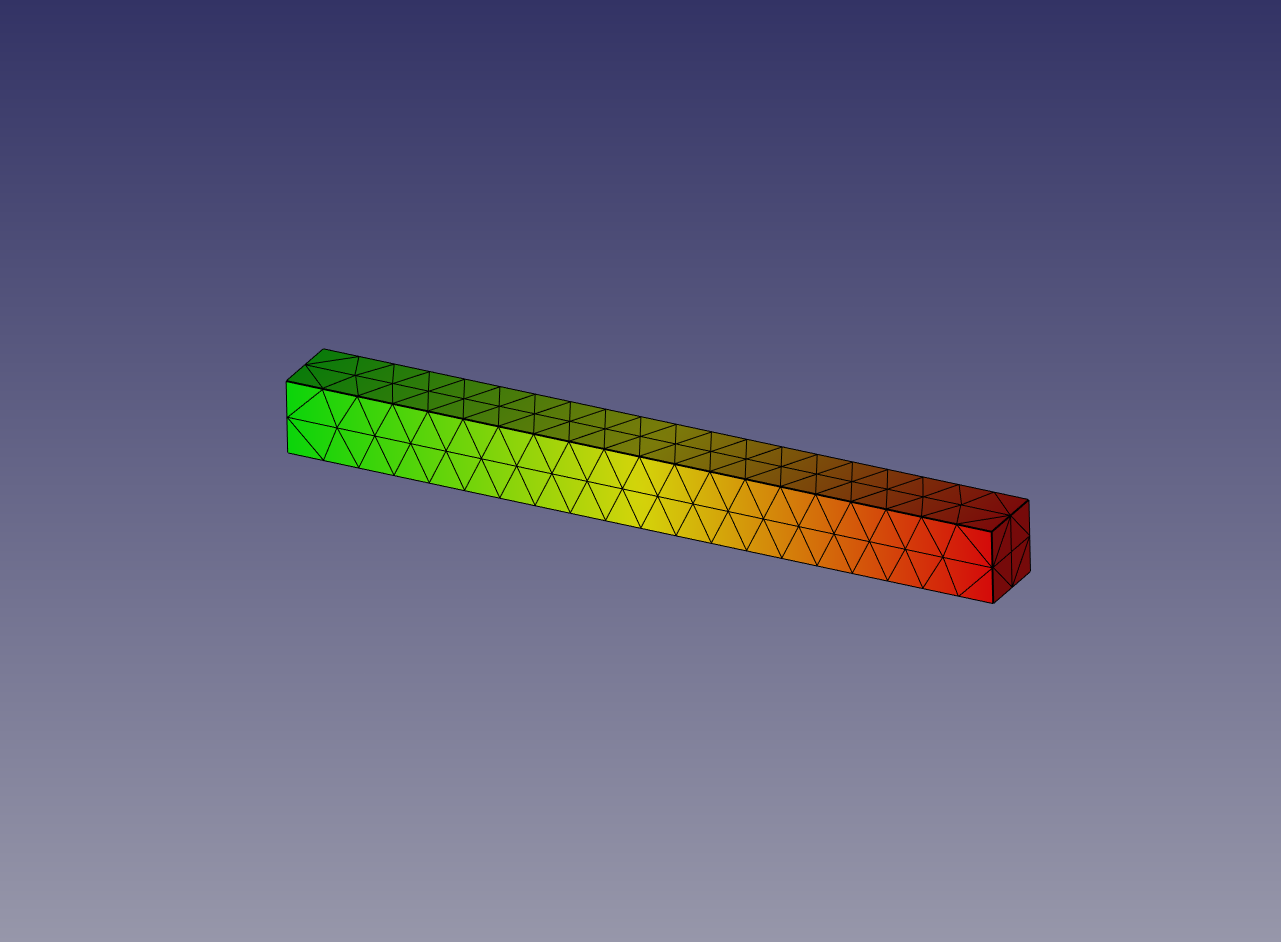
塑性考慮の場合には一定の応力下で変形し続けています。
作業 FreeCAD
c. SS線を定義
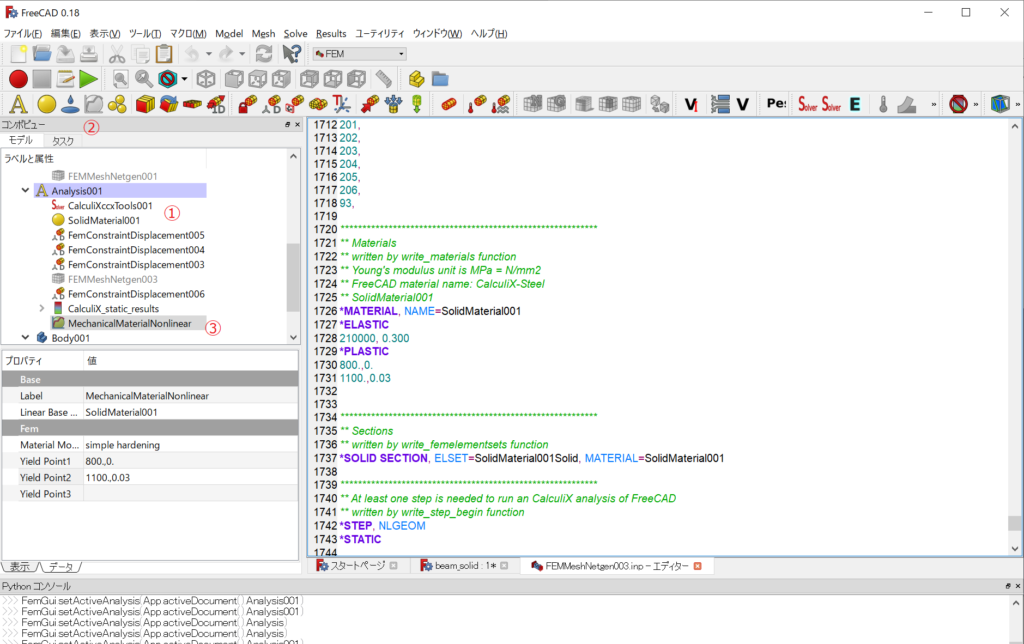
ツリーのマテリアルを選択する(①)と②の非線形材料の定義アイコンがアクティブになるので、クリックして③を選択しプロパティで設定します。
エディターで確認すると*ELASTICの下に*PLASTICコマンドと共に書き出されています。
*PLASTICは塑性変形部の情報を入力します。
b. Ramberg-Osgood 則の使用 については、エディターを編集することになります。
補足
そもそもRamberg-Osgood 則ですが、CCXのマニュアルには以下のようにあります。
\begin{align}
Eε = σ + α\Biggl( \frac{|σ|}{σ_0}\Biggl )^{n-1} σ
\end{align}
• *DEFORMATION PLASTICITY
Following line:
• Young’s modulus (E).
• Poisson’s ratio (ν).
• Yield stress (σ0)
• Exponent (n).
• Yield offset (α).
• Temperature.
試験データにうまく合わせればいいかと思います。
解析では変形量が大きくなっていますので、真ひずみで試験データを入力します。
\begin{align}
\small ε_t = Ln(1+ε_n)
\end{align}
\begin{align}
\small σ_t = σ_n(1+ε_n)
\end{align}
\begin{align}
\small ε_t:真ひずみ σ_t:真応力 ε_n:公称ひずみ σ_n:公称応力
\end{align}
サンプルファイル
(SS) beam_SS.inp
(Ramberg-Osgood) beam_RO.inp

コメント