陽解法のプログラムであるimpactを用いて梁の計算を行ってみました。A160のモデルに対して、境界条件を変えて実行しています。固定端の固定は変更せず(速度、加速度を0で固定)、たわみ端の負荷条件を変更しています。
荷重を加速度とする
\begin{align}\small F =ma\end{align}
\begin{align}\small a =\frac{F}{m}\end{align}
例題 A160に従って、荷重F=1000Nの時、0.01秒で1.9mmたわむ場合では、加速度a = 1000/3.59E-06 = 2.78E+08となり、拘束条件としてこの加速度を定義します。(質量m = 密度×体積/総節点数 = 7.9e-9 × 10000 / 22) 節点二箇所に負荷していますので、2.78E+08/2 = 1.39.E+08 を入力します。(accZ AZ = -139240506.3)
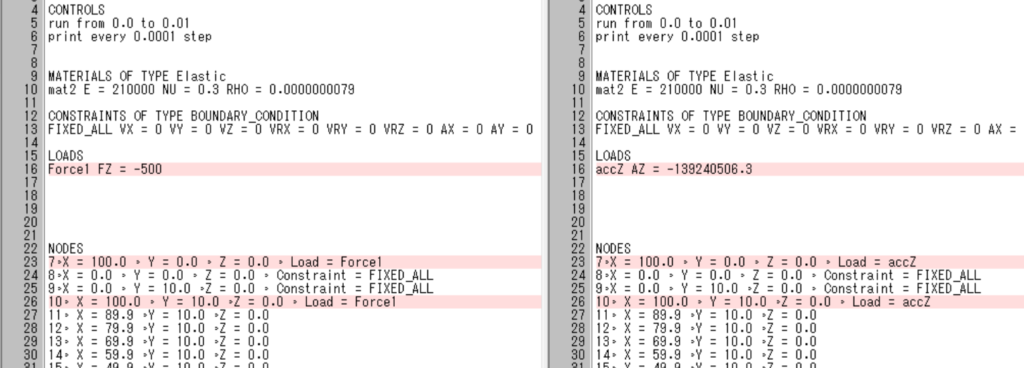
結果
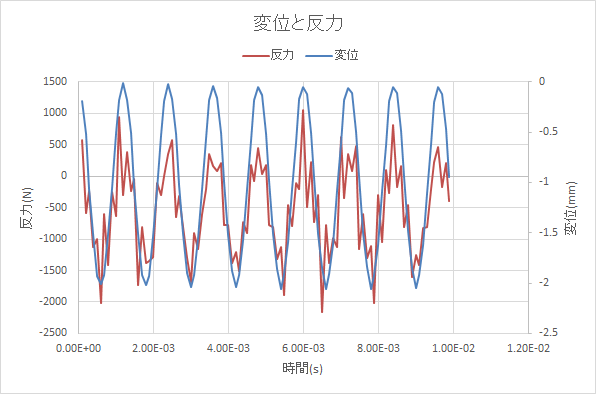
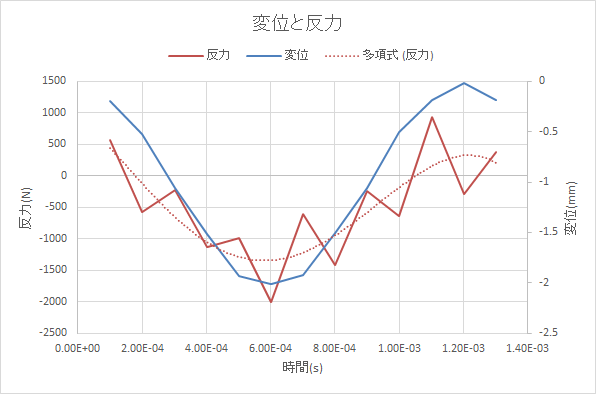
荷重1000Nを設定した場合とは異なり、衝撃力として作用していないようです。この設定は、重力等の体積力を定義するために使用されるので、このような使用は本来的なものではないようです。
拘束で加速度をつける
\begin{align}\small x =\frac{1}{2}at^2\end{align}
\begin{align}\small a =\frac{2x}{t^2}\end{align}
例題 A160に従って、1000Nの時、0.01秒で1.9mmたわむ場合では、加速度a = 2×1.9/0.01^2 = 38000となり、拘束条件としてこの加速度を定義します。(定義ブロックもloadから変更します)
CONSTRAINTS OF TYPE Boundary_Condition
Fixed_acc az = -38000
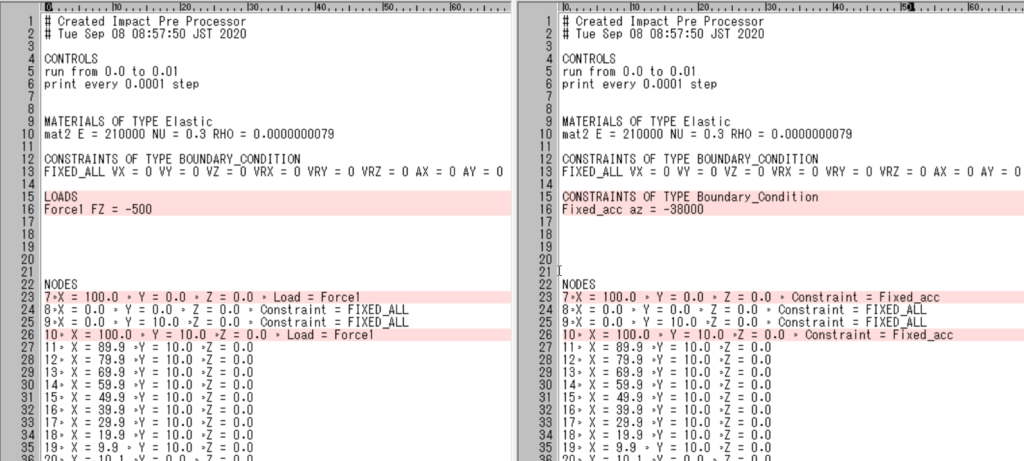
結果
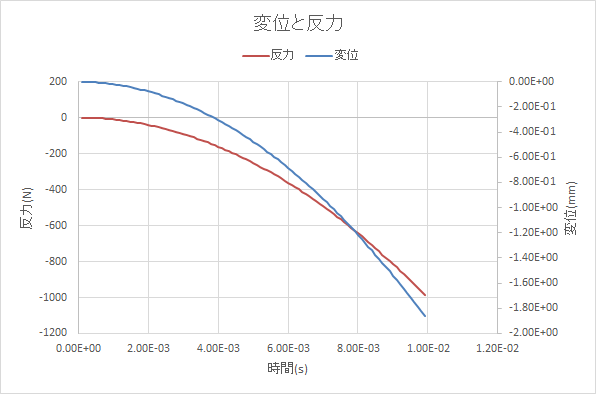
梁のたわみが1000Nで1.9mmになるような結果になっています。また放物線の形にもなっています。
節点の動きに対して拘束しているので、振動の成分は変位については無くなっており、反力の結果でもかなり小さくなっています。
拘束で速度をつける
\begin{align}\small x = vt\end{align}
例題 A160に従って、0.01秒で1.9mmたわむ場合では、速度v = 1.9/0.01 = 190 となり、拘束条件としてこの速度を定義します。
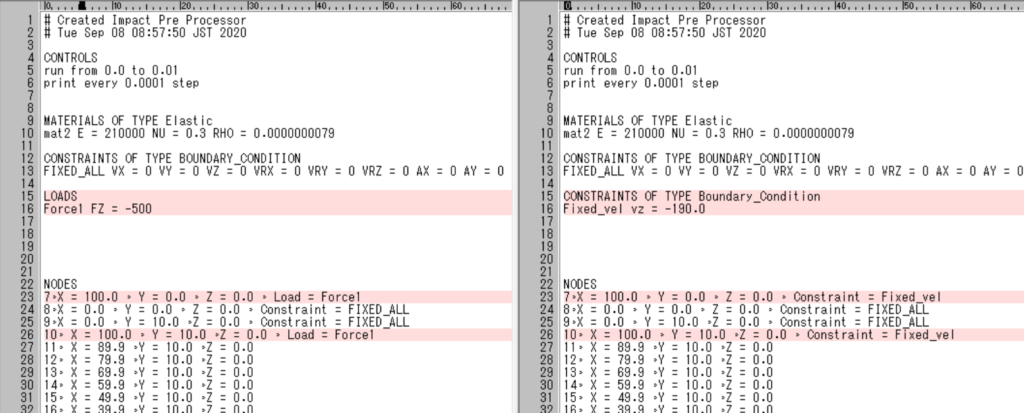
CONSTRAINTS OF TYPE Boundary_Condition
Fixed_vel vz = -190.0
結果
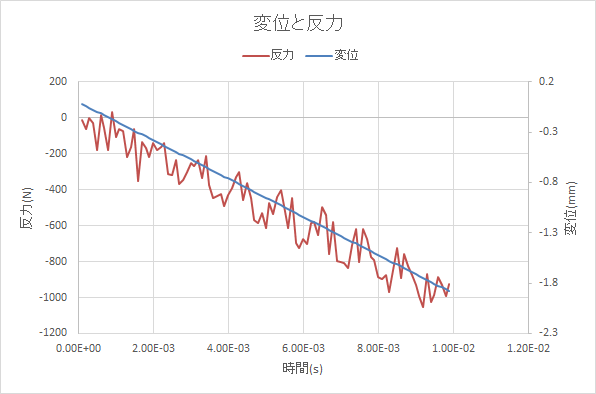
1.9mmたわんだ場合、1000N程度の反力となっています。振動成分は出ています。動解析で制動する場合には、速度でコントロールすることが多いかと思います。
コメント